浮動小数点数形式で数値を表す② IEEE754形式
IEEE754形式の浮動小数点数
限られた桁数でより大きな数値、小さな数値の実数を表すことが出来る浮動小数点数で
「IEEE754」(アイトリプルイーナナゴヨン)という形式に基づいた場合の表記方法についてメモします。
前回の記事で解説した通常の浮動小数点数形式(以降、通常形式と呼ぶ)とは正規化のルール及び、ビットへの格納時に処理が加わる点が異なります。
IEEE754の正規化と指数表記
例として10進数、0.375を指数表記を使って表します。
通常形式と同様、指数表記は2進数で行うため、「0.375」をあらかじめ2進数「0.011」へ変換しておく
指数表記

※指数表記は数値が2進数であることを表現するために以下の記述を行う場合もある
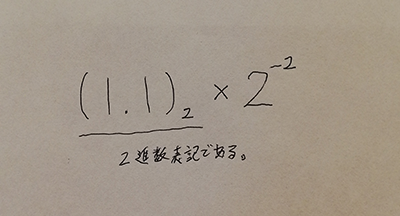
通常形式との違いは、
正規化で元の数値から小数点を移動させる際に、小数点の左側の整数部が0ではなく必ず1となるようにすること
IEEE754での正規化

仮数部は正規化後の数値「1.M」のMの部分にあたる。
(指数部、基数部、符号部は以下のように通常形式と同様)
指数部… 小数点の移動した数をマイナスで表す。
基数部… 2進数を扱っているため2で必ず固定される。
符号部… 数値が正の場合に0、負の場合に1となる。
32ビットに格納する
通常形式と同様、指数表記に変換した数値をビットに格納して浮動小数点数形式を表現する。
(符号部、指数部、仮数部を該当ビットに当てはめる)

先頭の符号部には正負を表すビットを格納。(今回は正を表す0)
指数部に127を足して格納する
指数部は通常形式と異なり、127を足してビットに格納する。(バイアス表現という)
通常指数は-128 ~ 127の範囲(符号つき2進数)で表すが、+127することにより 0 ~ 255の値(符号なし2進数)でビットに格納出来るようになる。
これにより負の数を含む表現が正の数だけで表せることが出来るため正負を考慮せずに指数の大小を比較することが可能になる。
今回の例では元の指数-2に127を足した結果の125を2進数に変換してビットに格納している

残りの仮数部は通常形式同様、指数表記の小数点以下の値を格納する。
IEEE754形式で正規化を行うことで整数部は必ず1となるのでそれをあえて格納しないことにより表現出来る桁を増やしている。


